TeX とはドナルド・クヌース氏の著書「TeXbook」の理論に基づく数学および科学文献のレイアウト用言語の総称で,主に学術論文など数式が配された文書の見栄えを良くする目的で作られ,数学記号の配置位置や間隔など様々なルールが盛り込まれています。つまりは,この言語を用いると印刷所の写植に出した際のような理想的な数式表示が期待できることから,組版もしくは清書言語とも呼ばれます。実に簡潔かつ平易なスタイルの言語で,特に専門的なコンピュータの知識やプログラム言語の知識を必要としないことから,パソコンは初心者という方でも習得するのはさして難しいことではありません。ドナルド・クヌース氏が自身の理論を具現化したのが,Plain TeX と呼ばれるフォーマットです。Plain TeX はフォントサイズに制限があるなど,実用性の面で難点がありました。このため,今日主流となっているLaTeX
などの発展型フォーマットが登場しました。しばしばTeX にはマクロが無く,LaTeX
で初めてマクロが追加されたかのように言われていますが,クヌース氏のPlain TeX にもマクロは組み込まれており,それは他のTeX フォーマットにも踏襲されています。
TeX の読み
TeX はギリシャ文字のタウ,イプシロン,カイの組み合わせのため,日本では一般的にギリシャ語読みの「テフ」と呼ばれていますが,英語圏では大多数が「テック」と呼びます。Plain-,AmS-,La- といった非ギリシャ語との組み合わせにおいては,後者の呼び名が自然に感じられますし,とりわけ海外での学術交流の際も役立つはずです。
LaTeX
TeX のフォーマットで最も普及しているのがLaTeX
で,一般的にTeX のコードといえば,おおかたLaTeX
のそれを指しています。またLaTeX
にはバージョンがあり,多くのケースで2.0.9 が使用されています。実は最新バージョンはLaTeX
2.0.9 をベースにした部分改良型のLaTeX
2e で,これが近く発表が予定されているLaTeX
3 までの繋ぎと考えられています。したがってLaTeX
2e はMathType の[切り取り/コピーの設定]ダイアログの[LaTeX
2.0.9 and later]にも該当します。一時は独自の規格を打ち出したアメリカ数学会もLaTeX
2e への切り換えを推奨しています。(ちなみに英語圏では一般的に「ラテック」あるいは「レイテック」と呼ばれます。)
TeX の数学記号
数学は古典ではなく,進化を続ける学問なので,それに用いられる記号も新たに作り出されてもいます。多くの研究者はTeX を使用しているので,それらの記号の大多数がTeX を使って表現できます。簡単に表現できない独創的な記号は,METAFONT というプログラムで,TeX 用の外字として作成することも可能ですが,簡単な合字であれば,通常のTeX の構文だけで表現できるものもあります。MathType には,数式に用いられるほとんどの記号をフォントとして有していますが,TeX による直接入力にも対応しているので,フォントの中にない記号も(TeX で表現できる限り)使用することができます。
記号 (右はMathJax での表示用)
|
意 味
|
TeX
|
|
|
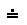 \(\doteq\)
|
同形(ほぼ等しい)
|
\doteq
|
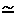 \(\simeq\)
|
漸進的に等しい
|
\simeq
|
 \(\because\)
|
理由・根拠
|
\because
|
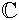 \(\mathbb{C}\)
|
シー(複素数の全体)
|
\mathbb{C}
|
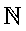 \(\mathbb{N}\)
|
エヌ(自然数の全体)
|
\mathbb{N}
|
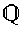 \(\mathbb{Q}\)
|
キュー(有理数の全体)
|
\mathbb{Q}
|
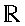 \(\mathbb{R}\)
|
アール(実数の全体)
|
\mathbb{R}
|
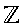 \(\mathbb{Z}\)
|
整数の全体
|
\mathbb{Z}
|
 \(\odot\)
|
丸中点演算子
|
\odot
|
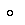 \(\circ\)
|
まる(合成写像)
|
\circ
|
 \(\vartriangleright\)
|
正規部分群として含む
|
\vartriangleright
|
 \(\triangleq\)
|
〜として定義する
|
\triangleq
|
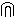 \(\Cap\)
|
二重インターセクション
|
\Cap
|
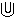 \(\Cup\)
|
二重ユニオン
|
\Cup
|
 \(\ddots\)
|
ドット右下がり
|
\ddots
|
 \(\dots\)
|
ドット下
|
\dots
|
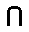 \(\bigcap\)
|
かつ, インターセクション, 積集合
|
\bigcap
|
 \(\cap\)
|
かつ, インターセクション, 積集合
|
\cap
|
 \(\mho\)
|
モー
|
\mho
|
 \(\cdots\)
|
ドット中央
|
\cdots
|
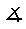 \(\measuredangle\)
|
計測済角
|
\measuredangle
|
 \(\cdot\)
|
ミディアムドット演算子, 乗法
|
\cdot
|
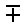 \(\mp\)
|
負または正符号
|
\mp
|
 \(\gg\)
|
非常に大きい
|
\gg
|
 \(\ll\)
|
非常に小さい, 絶対連続
|
\ll
|
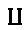 \(\coprod\)
|
集合としての直和
|
\coprod
|
 \(\vartriangleleft\)
|
〜の正規部分群
|
\vartriangleleft
|
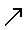 \(\nearrow\)
|
右上向矢印
|
\nearrow
|
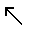 \(\nwarrow\)
|
左上向矢印
|
\nwarrow
|
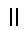 \(\parallel\)
|
並行
|
\parallel
|
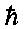 \(\hbar\)
|
エイチバー
|
\hbar
|
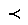 \(\prec\)
|
〜より好まれない
|
\prec
|
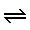 \(\rightleftharpoons\)
|
銛型右矢印・銛型左矢印
|
\rightleftharpoons
|
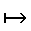 \(\mapsto\)
|
〜から(元の対応)
|
\mapsto
|
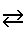 \(\rightleftarrows\)
|
右矢印左矢印
|
\rightleftarrows
|
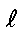 \(\ell\)
|
エル, リットル
|
\ell
|
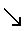 \(\searrow\)
|
右下向矢印
|
\searrow
|
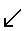 \(\swarrow\)
|
左下向矢印
|
\swarrow
|
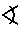 \(\sphericalangle\)
|
スヘリカルアングル
|
\sphericalangle
|
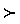 \(\succ\)
|
〜より好まれる
|
\succ
|
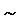 \(\sim\)
|
ティルド演算子, 相似
|
\sim
|
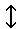 \(\updownarrow\)
|
上下矢印
|
\updownarrow
|
 \(\Updownarrow\)
|
上下両矢印
|
\Updownarrow
|
 \(\vdots\)
|
ドット縦
|
\vdots
|
 \(\bigcirc\)
|
円
|
\bigcirc
|
 \(\square\)
|
正方形
|
\square
|
 \(\triangle\)
|
三角形, デルタ
|
\triangle
|
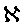 \(\aleph\)
|
アレフ(連続体濃度)
|
\aleph
|
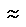 \(\approx\)
|
同形(ほぼ等しい)
|
\approx
|
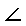 \(\angle\)
|
角
|
\angle
|
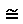 \(\cong\)
|
同形(ほぼ等しい)
|
\cong
|
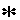 \(\ast\)
|
アスタリスク演算子, 乗法
|
\ast
|
 \(\bullet\)
|
ビュレット
|
\bullet
|
 \(\oplus\)
|
直和
|
\oplus
|
 \(\otimes\)
|
テンソル積, 直積
|
\otimes
|
 \(^\circ\)
|
度
|
^\circ
|
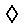 \(\diamond\)
|
ダイヤモンド演算子
|
\diamond
|
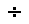 \(\div\)
|
割る(除算)
|
\div
|
 \(\cdot\)
|
ドット演算子
|
\cdot
|
 \(\downarrow\)
|
下向矢印
|
\downarrow
|
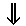 \(\Downarrow\)
|
下向二重矢印
|
\Downarrow
|
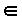 \(\in\)
|
〜に属する
|
\in
|
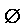 \(\varnothing\)
|
空集合
|
\varnothing
|
 \(\forall\)
|
普通限定子
|
\forall
|
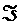 \(\Im\)
|
イマジナリーパート(虚部)
|
\Im
|
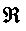 \(\Re\)
|
リアルパート(実部)
|
\Re
|
 \(\nabla\)
|
ナブラ
|
\nabla
|
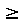 \(\geq\)
|
大なりイコール(大きいか, 等しい)
|
\geq
|
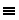 \(\equiv\)
|
合同, 恒等的に等しい
|
\equiv
|
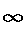 \(\infty\)
|
無限
|
\infty
|
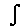 \(\int\)
|
インテグラル(積分)
|
\int
|
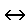 \(\leftrightarrow\)
|
同等
|
\leftrightarrow
|
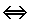 \(\Leftrightarrow\)
|
同値
|
\Leftrightarrow
|
 \(\langle\)
|
左山括弧(アングルブラケット)
|
\langle
|
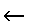 \(\leftarrow\)
|
左作用
|
\leftarrow
|
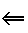 \(\Leftarrow\)
|
〜のために...
|
\Leftarrow
|
 \(\leq\)
|
小なりイコール(小さいか, 等しい)
|
\leq
|
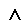 \(\wedge\)
|
ウエッヂ, 合接, 論理積
|
\wedge
|
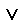 \(\vee\)
|
隣接, 論理和
|
\vee
|
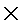 \(\times\)
|
かける(乗法)
|
\times
|
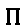 \(\prod\)
|
パイ(総乗)
|
\prod
|
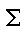 \(\sum\)
|
シグマ(総和)
|
\sum
|
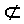 \(\not\subset\)
|
部分集合の否定
|
\not\subset
|
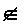 \(\notin\)
|
〜に属さない
|
\notin
|
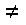 \(\neq\)
|
不一致
|
\neq
|
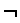 \(\neg\)
|
否定
|
\neg
|
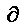 \(\partial\)
|
デル, 境界(偏微分)
|
\partial
|
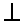 \(\bot\)
|
垂直
|
\bot
|
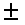 \(\pm\)
|
加法と減法
|
\pm
|
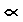 \(\propto\)
|
比例
|
\propto
|
 \(\rangle\)
|
右山括弧(アングルブラケット)
|
\rangle
|
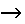 \(\rightarrow\)
|
右向矢印
|
\rightarrow
|
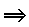 \(\Rightarrow\)
|
ならば(合意)
|
\Rightarrow
|
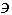 \(\backepsilon\)
|
リバースイプシロン
|
\backepsilon
|
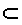 \(\subset\)
|
〜に含まれる
|
\subset
|
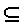 \(\subseteq\)
|
包含されるか, または同等
|
\subseteq
|
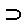 \(\supset\)
|
〜に含む
|
\supset
|
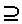 \(\supseteq\)
|
包含するか, または同等
|
\supseteq
|
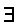 \(\exists\)
|
存在限定子
|
\exists
|
 \(\therefore\)
|
結論
|
\therefore
|
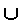 \(\cup\)
|
または, ユニオン
|
\cup
|
 \(\uparrow\)
|
上向矢印
|
\uparrow
|
 \(\Uparrow\)
|
上向二重矢印
|
\Uparrow
|
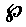 \(\wp\)
|
ワイエルシュトラスのP
|
\wp
|
|
|
WYSIWYG
WYSIWYG(ウィジウィグ)とはWhat You See Is What You Get の略で,TeX やhtml のエディターに多く見られる表現です。TeX は他の言語に比べ平易とはいえ,それで数式の個々の数字や記号の位置決めしなければならず,複雑化すると全体像を見失ってしまい,どの部分を作っているのかもわからなくなりがちです。それゆえ実際に印刷物上で表示される姿をモニターを通して確認できると作業もはかどりますが,それこそがWYSIWYG をうたったソフトウェアの存在意義でもあるのです。MathType の場合も,実際の数式の表示に変わってゆくのを観察しながら,直接ウインドウにTeX 入力できます。ただし数式以外のTeX コードは認識しません。またTeX においてWYSIWYG の表現については、DVI エディターが引き合いに出されがちです。DVIとはTeX の出力フォーマットで,PostScript やPDF への変換の際に用いますが,このコードはもはやTeX の原形をとどめない意味不明な文字の羅列と化します。
ちなみにMathType でDVI ファイルの表示はできません。
|